TL;DR: BucketList<T> is a data structure that performs exceptionally well for a certain usage scenario:

• n (list size) is large.
• Fast index-based access: list.GetItemAt(i).
• Fast index-based removal: list.RemoveAt(i).

In my use case, this reduced the runtime from 7 hours to 17 seconds!

An Interesting Problem

In December of last year I took part in solving the Advent of Code programming puzzles for the first time. Since then I became a bit obsessed with that and started solving also the older events going back until 2015.

Day 19 of 2016 presented an interesting challenge that took me a while to solve (with a reasonable runtime) and led to the solution based on this BucketList<T> data structure.

The basic idea behind this problem is that we have a:

• Circular data structure.
• Maintain a current element.
• Find the element opposite of the current element.
• Advance the current element by one.
• Repeat until the list has only one element left.

A poor solution

My first approach was using a LinkedList which performed OK for small list sizes. But for large lists (e.g. 3.001.330 was my puzzle input) the performance was dismal.

List size: 3001330.
END after 26696.1142087 seconds.

That's a runtime of more than 7 hours 😬.

The problem was the linear search for locating the opposite element in the list that caused an O(n²) complexity.

Using a simple List<T> (instead of LinkedList<T>) performed equally bad because in that case the remove operation causes a runtime complexity of O(n²).

To sum it up:

A better (by a lot) solution

So I needed a data structure with linear or better performance for:

• Indexing
• Removal

My solution was a custom data structure I called BucketList (ha ha) which:

• maintains the elements in a list of lists
• that have the same maximum size (hence, buckets).

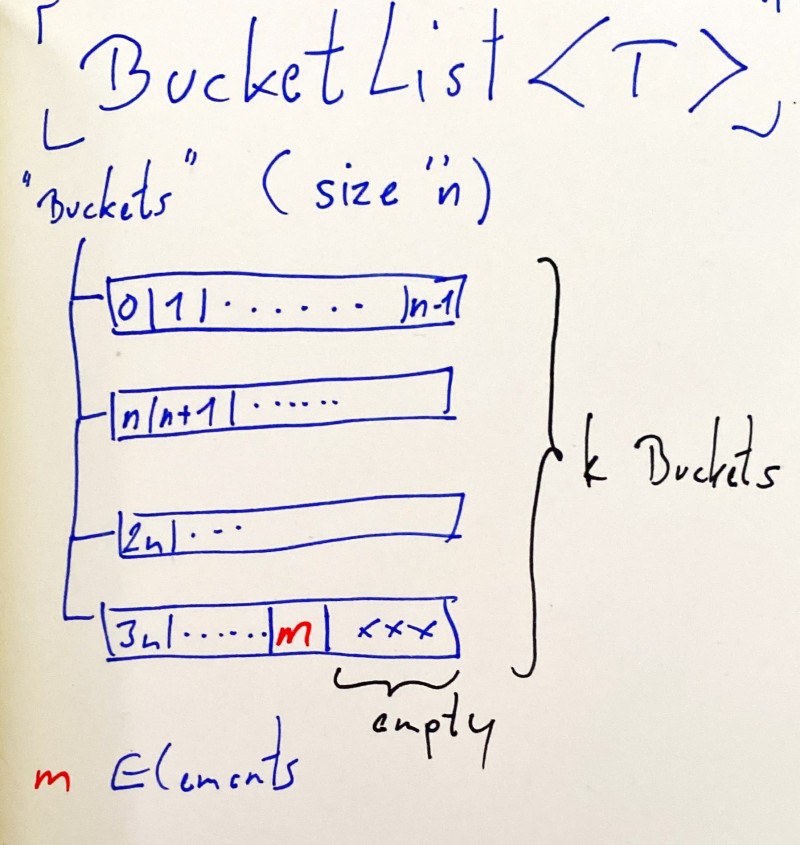
This way, when performing an index-based lookup I have nearly constant¹ O(1) access to elements and removal is only limited by the List<T> performance of a single bucket.

¹ Actually O(k) where k amounts to the number of buckets which should be negligibly low compared to n.

To sum it up:

k: number of buckets
n: bucket size (list size N / k)

This brought the runtime down dramatically!

List size: 3001330.
END after 17.0722168 seconds.

17 seconds ... way better 🤩.

Here's the full source code for BucketList.

Note: A bucket size of 25.000 worked best in that specific scenario but your mileage may vary, of course, and depends on the problem input size.

Caveats

• I only used BucketList<T> for this specific problem so far.
• The runtime performance depends on the selection of a bucket size for a given list size.
• The InsertAt case is not yet considered.
• I'm sure that this data structure exists already with a different name. However, I came up with this on my own when solving my problem, so give me that ;-).